Precej teles se vrti okoli stalne osi. Prikazano je kolo (disk) s polmerom 5.0 cm in maso 200 gramov, ki se s konstantno hitrostjo vrti okoli stalne osi (položaj je podan v centimetrih, čas je v sekundah).

V Predstavitvi 10.2 smo obravnavali, kakšna je odvisnost med linearno hitrostjo in kotno hitrostjo ter kakšna je odvisnost med kotnim pospeškom in kotno hitrostjo (α = Δω/Δt). V tej predstavitvi bomo obravnavali kinetično energijo vrtenja, W_{k rot} in vrtilno količino .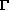

Obliko enačbe za kinetično energijo za vrtenje in vrtilno količino si lahko najlažje zapomnimo z analogijo s kinetično energijo premikanja in z gibalno količino. Spomnimo se, da velja W_k = 1/2 m v² in G = m v. Ali lahko uganeš, kakšen je izraz za vrtilno kinetično energijo in vrtilno količino?

Najprej, kaj bo pri pojmih o rotaciji igralo vlogo v in v? Pravilen odgovor je ω in ω. Če še ugotovimo, kaj igra vlogo m, dobimo vse potrebno. Lastnost mase je upiranje teles pri linearnem gibanju. Torej iščemo lastnost teles, ki opisuje njihovo upiranje pri rotaciji. Temu pravimo vztrajnostni moment. Vztrajnostni moment je odvisen od mase telesa, njegove velikosti in porazdelitve mase. Za najbolj preprosta telesa je vztrajnostni moment J = C m R², pri čemer je m masa telesa, R je njegova velikost (običajno polmer ali dolžina), C pa je brezdimenzijska konstanta, ki predstavlja porazdelitev mase.

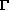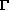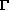Zato velja  W_{k rot} = 1/2 J ω² in  = J ω. Kolikšna sta W_{k rot} in  pri našem kolesu oziroma disku? No, iz Predstavitve 10.2 vemo, da velja ω = 1.256 radianov/s. Ker je naše kolo pravzaprav valj, je C = 1/2. Tako lahko izračunamo vztrajnostni moment kot: 2.5 x 10^-4 kg m². Končno imamo W_{k rot}  = 1.97 x 10^-4 J in  = 3.14 x 10^-4 Js (usmerjeno v zaslon računalnika). V našem primeru so te vrednosti majhne, saj je tudi J valja majhen. Valj s polmerom 1.0 m in maso 2.0 kg bi imel vztrajnostni moment enak 1.0 kg m².