Fourierjev teorem pravi, da lahko katerokoli periodično funkcijo predstavimo kot vsoto sinusnih valov. Včasih sicer ugotovimo, da potrebujemo neskončno sinusov, vendar lahko tako opišemo katerikoli periodični pojav. V tej animaciji bomo v luči Fourierjevega teorema raziskovali lihe periodične funkcije..  Ponovni zagon.

VSAKO liho periodično funkcijo x (perioda od L med 0 in L namesto -L/2 do L/2) lahko opišemo s členi Fourierjeve vrste kot:

 f(x) = Σ A_n sin (n*2*π*x/L),

V naši animaciji je L = 1. Enote so relativne. A_n je rezultat integrala, ki predstavlja prekrivanje med originalno funkcijo in določeno Fourierjevo komponento (člen v Fourierjevi vrsti, predstavljen s celim številom n). Za natančen izračun bi morali v integral vključiti 2/L (v našem primeru kar faktor 2, ker je L = 1). Ugotovimo, da je to potrebno z napovedjo A₃ za funkcijo sin(3*2*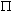*x) in nato to preverimo z animacijo.

Ne pozabi uporabljati pravilno sintakso, kot na primer  -10+0.5*t, -10+0.5*t*t  in  -10+0.5*t^2.

Preskusi različne lihe funkcije in opazuj rezultat integrala A_n.