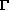 = r
× G. Iz tega izhaja, da je za izračun vrtilne količine za delec pomembno izhodišče.
Po preletu planeta klikni v posamezne "lonce".
= r
× G. Iz tega izhaja, da je za izračun vrtilne količine za delec pomembno izhodišče.
Po preletu planeta klikni v posamezne "lonce".
Vrtilna količina za delec je podana z vektorskim produktom 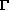 = r
× G. Iz tega izhaja, da je za izračun vrtilne količine za delec pomembno izhodišče.
Po preletu planeta klikni v posamezne "lonce".
= r
× G. Iz tega izhaja, da je za izračun vrtilne količine za delec pomembno izhodišče.
Po preletu planeta klikni v posamezne "lonce".
Med najbolj čudnimi mislimi o vrtilni količini je, da ima lahko telo vrtilno količino, če se giblje po premi črti. Vrtilna
količina za delec je podana z vektorskim produktom 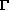 = r
× G. Iz tega izhaja, da je za izračun vrtilne količine za delec pomembno izhodišče.
= r
× G. Iz tega izhaja, da je za izračun vrtilne količine za delec pomembno izhodišče.
Če na sistem ne deluje zunanji navor, je vrtilna količina delca konstantna. V naši razpravi je delec prost, torej se vrtilna količina ohranja. Ali je kakšen drug način, da ugotovimo ohranitev vrtilne količine? Lahko. Pomislimo, če delec prekrije (glede na poljubno izhodišče) enako površino v enakih časovnih razmakih?
Ali v naši predstavitvi prekriva delec, ki se giblje po premi črti, enake površine v enakih časovnih razmikih?
Sproži animacijo in opazuj: Črna pika se prosto giblje od leve proti desni. Področja, ki jih prekrije delec glede na neko fiksno točko (izhodišče), so prikazana z različnimi barvami. Ali so vsa področja enako velika? Klikni na vsako posodo in opazuj, kaj se dogaja. Iz matematike vemo, da je površina trikotnika enaka produktu dolžine stranice in polovične višine na to stranico. Vsa področja imajo enako višino in dolžino stranice (= vx*dt).
Opomba: Keplerjev drugi zakon (glej poglavje 12 o podrobnostih o gravitaciji) pravi, da v enakih časovnih korakih vektor, ki izhaja iz Sonca proti nekemu planetu, prekrije enaka ploskovna področja. Kaj nam to pove o vrtilni količini planetov?