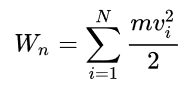
Pri tem je m masa molekule, vi pa njena hitrost.
Notranja energija idealnega plina je tudi proporcionalna absolutni temperaturi T:
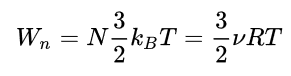
Pri tem je kb Boltzmannova konstanta in v število molov plina in R je splošna plinska konstanta
|
|
|
||||||||||||||||
|
|
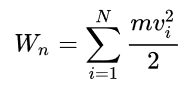
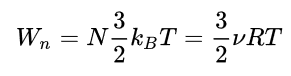
V tej animaciji velja, da je N = nR (številska vrednost Boltzmannove konstante je 1.38 10-23 J/K. R je univerzalna plinska konstanta 8310 J/K, T je absolutna temperatura v K, n je število molov snovi. Zaradi privzete vrednosti za kB je N potem številsko enak številu molekul v plinu.
Iz tega sledi plinska enačba za idealni plin v obliki pV = NT.. Prikazane povprečne vrednosti, < >, so izračunane preko intervalov ene časovne enote. Enote v simulaciji so J/K, K, m3 in J/m3 ter s za čas.
Temperatura plina je odvisna od notranje energije delcev. Pri enoatomarnih delcih je energija danega delca enaka njegovi kinetični energiji (vsaka prostostna stopnja prispeva 1/2 kBT in enoatomarni plin ima 3 prostostne stopnje). Zato ima idealen plin iz delcev enako povprečno energijo za vse delce.
Če potrojiš temperaturo, kaj se zgodi s kinetično energijo? Kaj se zgodi s hitrostjo delcev? Povprečna kinetična energija bi se morala povečati za trikrat, medtem ko se povprečna hitrost delcev poveča za 1.73-krat, kar je kvadratni koren od 3.