Predstavitev podatkov v računalniku
Računalnik uporablja določeno število bitov, da predstavlja nek podatek,
ki je lahko število, znak ali kaj drugega. n-bitno mesto shranjevanja
lahko predstavlja do 2n ločenih entitet. Na primer, 3-bitna
pomnilniška lokacija lahko vsebuje enega od naslednjih osem binarnih
vzorcev: 000, 001, 010, 011, 100, 101, 110 ali 111. Zato lahko
predstavlja največ 8 ločenih entitet. Lahko jih uporabimo za
predstavljanje številk od 0 do 7, številk od 8881 do 8888, znakov „A“ do
„H“ ali do 8 vrst sadja, kot so jabolka, pomaranča, banana itd., ali do 8
vrst živali, kot so lev, tiger itd.
Cela števila so lahko predstavljena na primer z 8-biti,
16-biti, 32-biti ali 64-biti. Kot programer lahko izberemo ustrezno
dolžino bitov za naša cela števila. Ta izbira bo omejila obseg celih
števil, ki jih je mogoče predstaviti.
|
Poleg bitne
dolžine je lahko celo število predstavljeno v različnih
predstavitvenih shemah, npr. nepredznačena ali predznačena cela
števila (cela števila s predznakom ali brez njega).
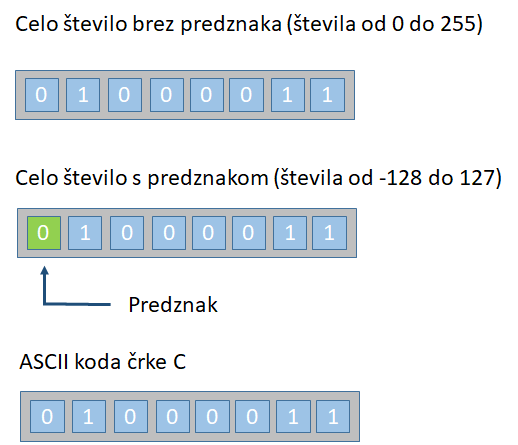
8-bitno nepredznačeno celo število ima razpon od 0 do 255, medtem ko
ima 8-bitno celo število s predznakom razpon od -128 do 127. Obe
obliki predstavlja 256 različnih števil.
Pomembno je omeniti, da je lokacija v pomnilniku računalnika
samo za shranjevanje binarnega vzorca. Kot programer se odločimo,
kako si tak vzorec razlagamo.
Na primer, 8-bitni binarni vzorec "0100 0001B" je mogoče
razlagati kot nepredznačeno celo število 67 ali znak ASCII "A" ali
kakšen tajni, ki ga razumemo samo mi. Z drugimi besedami se moramo
najprej odločiti, kako predstaviti del podatkov v binarnem vzorcu,
preden ti binarni vzorcidobijo nek smisel. |
Interpretacija binarnega vzorca se imenuje predstavitev podatkov ali
kodiranje. Pomembno je, da se vsi dogovorimo o obliki predstavitve
podatkov, tj., da upoštevamo veljavne standarde.
Predstavitev celih števil
Cela števila in realna števila predstavljamo v računalnikih
različno. Za delo z realnimi števili imamo v računalniku tudi
poseben namenski procesor za delo z realnimi števili (ali bolje s
števili s plavajojo decimalno vejico).
Pogosto uporabljene bitne dolžine lokacij za pomnenje celih števil so 8,
16, 32 ali 64 bitov. Števila imajo lahko predznak ali pa tudi ne.
n-bitna cela števila brez predznaka
Tako kodiranje števil porabi vseh n bitov za vrednost števila in ne
dopušča predznaka. Glede na številom n bitov imamo naslednje
možnosti:
| Število bitov (n) |
Minimum |
Maksimum |
| 8 |
0 |
28-1 = 255 |
| 16 |
0 |
216-1 =65535 |
| 32 |
0 |
232-1 =4294967295 ( več kot 9 mest) |
| 64 |
0 |
264-1 =18446744073709551615 (več kot 19 mest) |
Cela števila s predznakom
Predznačena števila imajo poleg ničle in pozitivnih vrednosti lahko tudi
negativne. Najbolj pomemben (levi) bit je namenjen predznaku. Vrednost
tega bita 0 pomeni pozitivno število, vrednost 1 pa negativno. Na
voljo imamo naslednje predstavitve:
- Predstavitev s predznakom
in absolutno vrednostjo
- predstavitev z eniškim
komplementom
- predstavitev z dvojiškim
komplementom
|
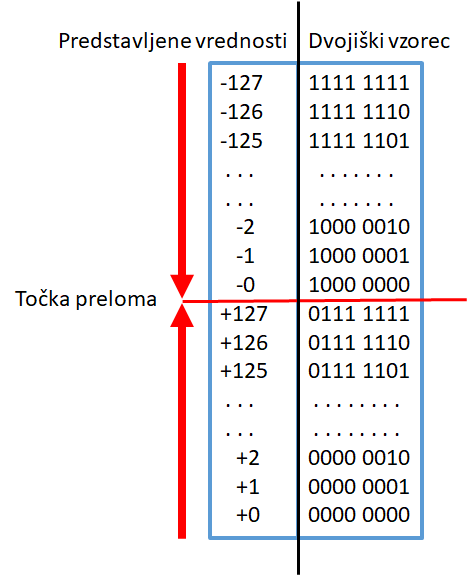
Predstavitev s predznakom in absolutno vrednostjo
|
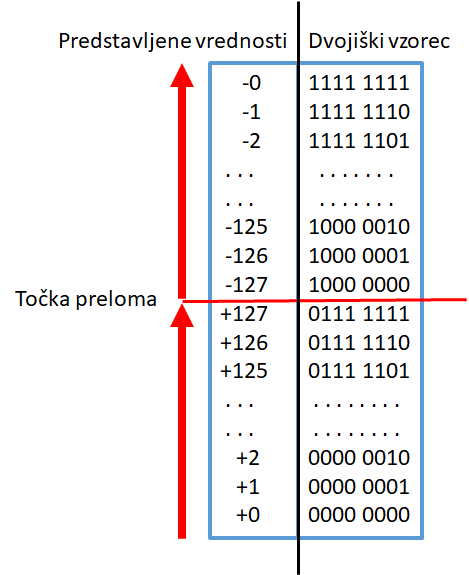
Predznačena cela števila in eniški komplement
|
|
 |
|
|
Slabosti:
- dve predstavitvi ničle (0000 0000B in 1000 0000B)
.
- pozitivna in negativna moramo števila obravnavati
ločeno.
|
Slabosti:
- dve predstavitvi ničle (0000 0000B in 1111 1111B)
.
- pozitivna in negativna moramo števila obravnavati
ločeno.
|
|
Predznačena cela števila in dvojiški komplement

|
- Spet je najbolj levi bit za predznak. Preostalih n-1 bitov
predstavlja absolutno vrednost števila na naslednji način:
- Za pozitivna števia je absolutna vrednost enaka vrednosti
vzorca n-1 bitov.
- Za negativna cela števila je absolutna vrednost števila
enaka komplementu (n-1) bitnega vzorca plus 1
(zato dvojiški komplement).
|
Prednosti:
- Z dvojiškim komplementom ima ničla le eno predstavitev.
- Seštevanje in odštevanje negativnih in pozitivnih števil poteka z isto
logiko.
Zato računalniki uporabljajo za predstavitev predznačenih celih števil
dvojiški komplement!
V naslednjih primerih predpostavimo, da za pomnenje števil uporabimo po 8
bitiov (n=8):
Primer 1: Seštevanje dveh pozitivnih števil: 65 + 5 = 70
dvojiško:
0100 000 + 0000 0101 = 0100 0110
Primer 2: Odštevanje je v bistvu seštevanje pozitivnega in
negativnega števila: 65 - 5 = 60
Dvojiško: 0100 0001 - 0000 0101 = 0100 0001 +
1111 1011 = 0011 1100
Primer 3: Seštevanje dveh negativnih števil: -65 -5 = -70
Dvojiško:
1011 1111 + 1111 1011 = 1011 1010
Območje predznačenih celih števil z dvojiškim komplementom
| n bitov |
minimum |
maximum |
| 8 |
-(27) (=-128) |
+(27)-1 (=+127) |
| 16 |
-(215) (=-32768) |
+(215)-1 (=+32767) |
| 32 |
-(231) (=-2147483,648) |
+(231)-1 (=+2147483647)(več kot 9 mest) |
| 64 |
-(263) (=-9223372036854775,808) |
+(263)-1 (=+9223372036854775,807)(več
kot 18 mest) |
Dekodiranje števil z dvojiškim komplementom
- Preveribi bit za predznak (označen kot S).
- Če S=0, je število pozitivno in njegova absolutna vrednost je kar
dvojiška vrednost preostalih n-1 bitiv.
- Če S=1, je število negativno. Absolutno vrednost dobimo z inverzijo
preostalih n-1 bitov, katerim prištejemo 1.
Pravilo debelega in tenkega konca (Big Endian : Little Endian)
- naslov
sestavljenega operanda je enak naslovu besede, ki vsebuje najtežji
(največ vreden) del operanda
Sodobni računalniki pomnijo na vsaki naslovljeni lokaciji1 bajt. Za 32
bitno celo število tako porabimo 4 pomnilne lokacije oziroma naslove.
Izraz konec ("Endian") govori o vrstnem redu shranjevanja baytov v
pomnilnik. Če imamo shemo "Big Endian" (torej debeli konec), je najbolj
pomemben bajt shranjen na najnižjem naslovu (torej: najprej največji). Pri
shemi "Little Endian" pa shranimo na najnižji naslov najmanj pomemben
bajt.
Primera: 32 bitno celo število 12345678(šestnajstiško)
lahko pomnimo kot 12H 34H
56H 78H po shemi debelega konca ali kot 78H
56H 34H 12H pp shemi tenkega konca.
16bitno celo število 00H 01H razumemo kot 000(šestnajstiško)
po shemi debelega konca in kot 0100(šestnajstiško) po shemi
tankega konca.
Predstavitev realnih števil
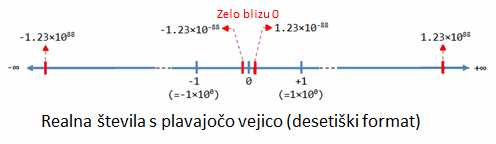 |
Realno
število (oziroma število s plavajočo vejico) lahko predstavlja
zelo veliko vrednost (n.pr 1.23 *1088) ali zelo
majhno (n.pr. 1.23 *10-88) . Lahko predstavlja tudi zelo
veliko negativno vrednost (-1.23*1088) ali zelo majhno
negativno (primer: -1.23*10-88), pa tudi 0: |
Realna števila pogosto prikazujemo z znanstveno notacijo z mantiso
(oziroma frakcijo, F) in eksponentom (E) z določeno bazo (r) v
obliki
F* rE.
Decimalna števila uporabljajo bazo 10 (F*10E) , dvojiška pa
bazo 2 (F*2E ).
Predstavitev realnih števil ni unikatna. Število 55.66 lahko
zapišemo tudi kot 5.566* 101, 0.5566*102, 0.05566*
103 itd. Del s frakcijo lahko normaliziramo. V normalizirani
obliki imamo pred (decimalno) piko le eno števko, različno od 0. Tako na
primer desetiško število 123.4567 normaliziramo kot
1.234567*102; Dvojiško število 1010.1011B bi
normalizirali kot 1.0101011B*23.
Velja omeniti, da realna števila zaradi fiksnega števila bitiov (na
primer, 32 ali 64 bitov) izgubijo na natančnosti. Tako imamo na primer že
v majhnem intervalu med 0.0 do 0.1 neskončno vrednosti realnih števil. Po
drugi strani pa imamo pri n bitnem vzorcu le 2n različnih
vzorcev. Torej ne moremo predstaviti vseh realnih števil. Uporabiti bomo
morali približke.
Velja še omeniti, da je aritmetika s plavajočo vejico bolj počasna
od celoštevilčne aritmetike. Če se le da, raje uporabljajmo cela števila.
V računalnikih uporabljamo za realna števila znanstveno notaciji z
bazo 2. Za predstavitev enega realnega števila običajno uporabljamo
32 bitov (za enojnio natančnost) ali 64 bitov (za dvojno natančnost).
32-bitna števila s plavajočo vejico in enojno natančnostjo
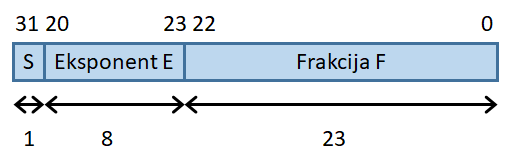 |
- Najbolj pomemben bit pomeni predznak (S), ki je 0 za pozitivna
in 1 za negativna števila.
- Naslednjih 8 bitov je eksponent (E).
- Preostalih 23 bitov je frakcija (F).
|
Normalizirana oblika
Kot zgled vzemimo 32 bitni vzorec 1 1000 0001 011 0000 0000
0000 0000 0000; torej je :
- S = 1
- E = 1000 0001
- F = 011 0000 0000 0000 0000 0000
V normalizirani obliki je aktualna frakcija normalizirana z implicitno
vodečo enko (1) in ima obliko 1.F. V našem primeru je zato dejanska
frakcija
1.011 0000 0000 0000 0000 0000 = 1 + 1*2-2 + 1*2-3
= 1.375(desetiško).
Bit za predznak je S=1, torej imamo negativno število: -1.375(desetiško).
V normalizirani obliki je aktualni eksponent E-127 (takoimenovani
odmik -127). To je zato, ker moramo predstavljati tako pozitivne kot
negativne eksponente. Ker imamo pri 8 bitih območje od 0 do 255, omogoča
odmik-127 dejanske eksponente med -127 in 128. V našem primeru je
E-127=129-127=2(desetiško).
Torej je predstavljeno število : -1.375* 22=-5.5(desetiško).
Denormalizirana oblika
Normalizirana oblika ima problem zaradi vodeče 1 za frakcijo. Zato
ne more predstaviti števila 0.
Za E=0, uporabimo zato denormalizirano obliko. Za frakcijo uporabimo
implicitno vodečo 0 (namesto 1). Aktualni eksponent je vedno -126.
Nič zato predstavimo z E=0 in F=0 (saj velja 0.0*2-126=0).
V denormalizirani obliki lahko prikazujemo tudi zelo majhna negativna ali
pozitivna števila.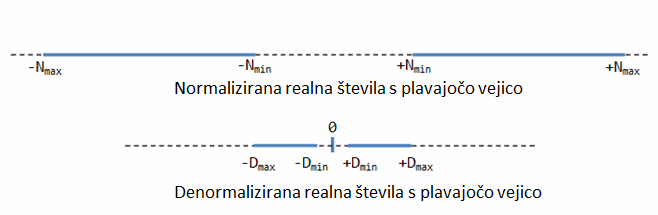
64-bitna števila s plavajočo vejico in dvojno natančnostjo
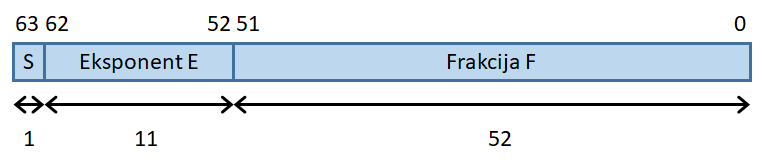 |
- Najbolj pomemben bit pomeni predznak (S), ki je 0 za pozitivna
in 1 za negativna števila.
- Naslednjih 11 bitov je eksponent (E).
- Preostalih 52 bitov je frakcija (F).
|
Vrednost N računamo tako:
- Normalizirana oblika: Za 1 ≤ E ≤ 2046: N = (-1)S *1.F
* 2(E-1023)
- Denormalizirana oblika: Za E = 0: N = (-1)S * 0.F *
2(-1022)
- Za E = 2047, N predstavlja posebne vrednosti, kot so
represents special values, neskončno (infinity) in NaN (not a
number, ni število).
Še primerjava normaliziranih minimalnih in maksimalnih možnih vrednosti v
enojni ali dvojni natančnosti:
| Natančnost |
Normalizirana N(min) |
Normalizirana N(max) |
| Enojna (Single) |
0080 0000 (šestnajstiško)
= 0 00000001 00000000000000000000000
E = 1, F = 0
N(min) = 1.0 * 2-126
(≈1.17549435 * 10-38 |
7F7F FFFF(šestnajstiško)
= 0 11111110 00000000000000000000000
E = 254, F = 0
N(max) = 1.1...1 * 2127 = (2 - 2-23) * 2127
(≈3.4028235 * 1038) |
| Dvojna (Double) |
0010 0000 0000 0000(šestnajstiško)
N(min) = 1.0 * 2-1022
(≈2.2250738585072014 * 10-308) |
7FEF FFFF FFFF FFFF(šestnajstiško)
N(max) = 1.1...1 * 21023
= (2 - 2-52) * 21023
(≈1.7976931348623157 * 10308) |
Denormalizirane vrednosti pa so za zelo majhne vrednosti blizu ničle in
ki ne morejo bito normalizirane:
| Natančnost |
Denormaliziran D(min) |
Denormaliziran D(max) |
| Enojna (Single) |
0000 0001 (šestnajstiško)
0 00000000 00000000000000000000001
E = 0, F = 00000000000000000000001
D(min) = 0.0...1 * 2-126 = 1 * 2-23 * 2-126
= 2-149
(≈1.4 * 10-45) |
007F FFFF(šestnajstiško)
0 00000000 11111111111111111111111
E = 0, F = 11111111111111111111111
D(max) = 0.1...1 * 2-126 = (1-2-23)*2-126
(≈1.1754942 * 10-38) |
| Dvojna (Double) |
0000 0000 0000 0001(šestnajstiško)
D(min) = 0.0...1 * 2-1022 = 1 * 2-52 * 2-1022
= 2-1074
(≈4.9 * 10-324) |
001F FFFF FFFF FFFF(šestnajstiško)
D(max) = 0.1...1 * 2-1022 = (1-2-52)*2-1022
(≈4.4501477170144023 * 10-308)
|
Kodiranje znakov
V pomnilniku računalnika so znaki "zakodirani" s pomočjo izbrane kodirne
sheme. Med bolj pogostimi shemami kodiranja znakov so: 7 bitni
ASCII, 8 bitni Latin-x in Unicode.
7 bitna shema ASCII lahko predstavlja 128 znakov. 8 bitna shema (na
primer Latin-x) lahko predstavlja 256 znakov. 16bitne sheme (kot na primer
Unicode UCS-2) lahko obsega 65536 znakov.
7-bitna koda ASCII
- ASCII je med starejšimi kodnimi shemami. Kasneje so jo razširili na 8
bitov.
- Kode 32 do 132 (desetiško) oziroma 20 do 7E (šestnajstiško) so
uporabljene za znake, ki jih lahko prikažemo (natisnemo) v skladu z
naslednjima tabelama:
| hex |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
| 2 |
SP |
! |
" |
# |
$ |
% |
& |
' |
( |
) |
* |
+ |
, |
- |
. |
/ |
| 3 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
: |
; |
< |
= |
> |
? |
| 4 |
@ |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
| 5 |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
[ |
\ |
] |
^ |
_ |
| 6 |
` |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
| 7 |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
{ |
| |
} |
~ |
|
|
| Dec |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 3 |
|
|
SP |
! |
" |
# |
$ |
% |
& |
' |
| 4 |
( |
) |
* |
+ |
, |
- |
. |
/ |
0 |
1 |
| 5 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
: |
; |
| 6 |
< |
= |
> |
? |
@ |
A |
B |
C |
D |
E |
| 7 |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
| 8 |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
| 9 |
Z |
[ |
\ |
] |
^ |
_ |
` |
a |
b |
c |
| 10 |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
| 11 |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
| 12 |
x |
y |
z |
{ |
| |
} |
~ |
|
|
|
|
Kode 0D (00H) do 31D (1FH) in
127D (7FH) so rezervirane za posebne znake, ki jih
ne moremo prikazati oziroma natisniti.
| DEC |
HEX |
Pomen |
DEC |
HEX |
Pomen |
| 0 |
00 |
NUL |
Null |
17 |
11 |
DC1 |
Device Control 1 |
| 1 |
01 |
SOH |
Start of Heading |
18 |
12 |
DC2 |
Device Control 2 |
| 2 |
02 |
STX |
Start of Text |
19 |
13 |
DC3 |
Device Control 3 |
| 3 |
03 |
ETX |
End of Text |
20 |
14 |
DC4 |
Device Control 4 |
| 4 |
04 |
EOT |
End of Transmission |
21 |
15 |
NAK |
Negative Ack. |
| 5 |
05 |
ENQ |
Enquiry |
22 |
16 |
SYN |
Sync. Idle |
| 6 |
06 |
ACK |
Acknowledgment |
23 |
17 |
ETB |
End of Transmission |
| 7 |
07 |
BEL |
Bell |
24 |
18 |
CAN |
Cancel |
| 8 |
08 |
BS |
Back Space '\b' |
25 |
19 |
EM |
End of Medium |
| 9 |
09 |
HT |
Horizontal Tab '\t' |
26 |
1A |
SUB |
Substitute |
| 10 |
0A |
LF |
Line Feed '\n' |
27 |
1B |
ESC |
Escape |
| 11 |
0B |
VT |
Vertical Feed |
28 |
1C |
IS4 |
File Separator |
| 12 |
0C |
FF |
Form Feed 'f' |
29 |
1D |
IS3 |
Group Separator |
| 13 |
0D |
CR |
Carriage Return '\r' |
30 |
1E |
IS2 |
Record Separator |
| 14 |
0E |
SO |
Shift Out |
31 |
1F |
IS1 |
Unit Separator |
| 15 |
0F |
SI |
Shift In |
|
|
|
|
| 16 |
10 |
DLE |
Datalink Escape |
127 |
7F |
DEL |
Delete |
Na osnovi 7-bitne ASCII tabele so razvili različne druge, ki vključujejo
jezikovne posebnosti. Tako je danes poleg ASCII najbolj znana družina
kodirnih tabel ISO-Latin, ki ima 8 bitov. ISO Latin 1 (tudi IS0 8859-x) je
družina kodirnih tabel, ki vključuje nacionalne posebnosti - razširitev
osnovnega ASCII nabora. V verziji ISO-8859-2 najdemo tudi šumnike.
Unicode ( Universal Character Set)
Unicode naj bi omogočala kodiranje znakov, ki jih zasledimo tudi v drugih
jezikih. Je pa skladna s starejšimi shemami, saj prvih 128 znakov
uporablja iste kode kot ASCII, prvih 256 znakov pa upošteva standard
Latin-1 (namenjen zahodnim pisavam).
UTF-8 (Unicode Transformation Format - 8-bitni)
16/32 bitna shema Unicode je zelo neučinkovita, če dokumenti vsebujejo
pretežno znake ASCII, saj za vsak znak porabimo 2 bajta. UTF-8
sodi med kodirne sheme spremenljive dolžine (za vsak znak 1 do 4 bajti). V
UTF-8 uporabljamo za pogosto znane znake, skladne z ASCII, le po 1 bajt.
Redko uporabljani znaki pa porabijo do 4 bajte.
Preslikava med shemama Unicode in UTF-8 je naslednja:
| Biti |
Unicode |
UTF-8 Code |
Bajtov |
| 7 |
00000000 0xxxxxxx |
0xxxxxxx |
1 (ASCII) |
| 11 |
00000yyy yyxxxxxx |
110yyyyy 10xxxxxx |
2 |
| 16 |
zzzzyyyy yyxxxxxx |
1110zzzz 10yyyyyy 10xxxxxx |
3 |
| 21 |
000uuuuu zzzzyyyy yyxxxxxx |
11110uuu 10uuzzzz 10yyyyyy 10xxxxxx |
4 |
UTF-16 in UTF-32
UTF-16 je tudi shema s spremenljivo dolžino, ki uporablja 2 do 4 bajte.
Ta shema je bolj redko uporabljena. Imamo tudi 32 bitno shemo UTF-32.
Formati tekstovnih datotek z več bajti (n.pr., Unicode)
Vrstni red bajtov: Pri znakih, ki potrebujejo več bajtov, moramo
paziti na zaporedje teh bajtov v pomnilniku. Če uporabljamo pravilo
debelega konca (big endian), je najbolj pomemben bajt shranjen na
pomnilniški lokaciji z najnižjim naslovom (najprej najbolj pomemben bajt).
Pri pravilu tankega konca (little endian) je najbolj pomemben byte na
lokaciji z najvišjim naslovom. Pravilo debelega konca tvori bolj berljiv
šestnajstiški prikaz in je bolj pogosto.
BOM (Byte Order Mark): BOM je posebna Unicode koda z vrednostjo
FEFFH, po kateri ločimo debeli konec od tankega. Za slednjega
ima BOM vrednost FF FEH.BOM se kot ene vrste podpis
pojavlja na začetku tekstovne datoteke.







